The map of a city consists of streets and intersections.
All streets are oriented either horizontally or vertically. A street starts and ends at some intersection, but may have other intersections in between.
Every street has a different name and every intersection has a unique number assigned to it.
The map is described as a list of tuples of size 4. In each tuple,
-
The first two elements a,b are integers denoting the intersections.
-
The third element is the name of the street that goes through the intersections a,b.
-
The fourth element is a character (either 'N', 'S', 'W' or 'E') denoting the direction of the street from a to b, which means that the street starts from a to b and goes in the direction 'd'. ('N', 'S', W' and 'E' represent north, south, west and east respectively).
-
There are no intersections in between a and b, i.e. the tuple represent segments of the street. See the figure below for more clarity
It is guaranteed that for every intersection, not more than 4 streets pass through it and every street is a straight line, i.e. streets are either completely horizontal or completely vertical.
Find the number of (unordered) pairs of streets that cross each other.
Two streets cross each other if there is an intersection such that the both streets pass through through the intersection, but do not start or end at it.
An example is the following,
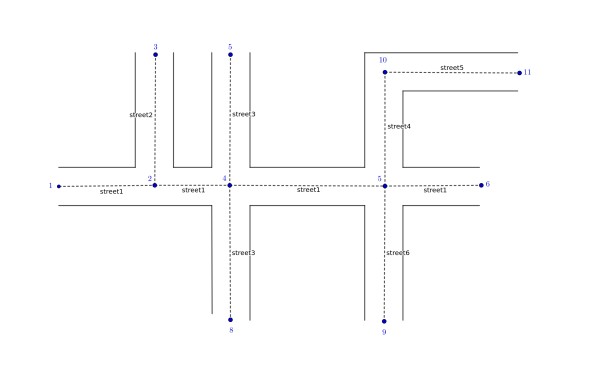
The intersections are 1,2,…11
The street names are given beside each segment.
The only pair of streets that cross each other is the pair ('street1', 'street3'). See explanation section for more details.
INPUT
-
The first line contains one single integer, n the number of tuples through which the map is specified.
-
The next n lines each contain the four elements of the tuple separated by a space.
More specifically,
-
The first two space separated integers are the intersection numbers (integers from 0 to 10^5)
-
This is followed by a space and a string with alphanumeric characters, the street name (not exceeded 100 characters in length)
-
This is followed by a space and a character among {'N', 'S', 'E', 'W'}, the direction of the street from the first intersection to the second.
OUTPUT
Print in a single line the number of pairs of streets that cross each other.
Constraints
Sample Input
10
1 2 street1 E
2 3 street2 N
7 4 street3 S
2 4 street1 E
4 5 street1 E
6 5 street1 W
5 10 street4 N
5 9 street6 S
10 11 street5 E
4 8 street3 S
Sample Output
1
Explanation
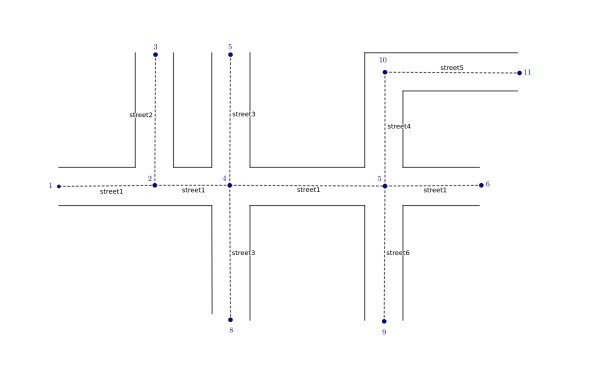
The above figure depicts the sample input.
Only the streets street3 and street1 cross each other.
Although street2 and street1 intersect, they do not cross each other since street4 ends where they meet.
Although street4 and street1 intersect, towards the South of the intersection point 5, street6 starts and so they do not cross each other.
So the answer is 1.
Time Limit: 1 secs